Vom Bit zum Wort: Computer und Daten
Der folgende Artikel behandelt die Art, wie Computer (PCs) Daten speichern. In Form einer kurzen Übersicht werden Zahlensysteme, Speicherformate und logische Operationen dargestellt sowie eine Vielzahl von Fachbegriffen erklärt.
Binär: Ja oder Nein
Computer arbeiten bekanntlich digital, was bedeutet, dass alle Informationen durch Zahlen repräsentiert werden. 1 Der Gegensatz hierzu ist eine analoge Arbeitsweise. Wer diese Begriffe veranschaulicht haben möchte, werfe einen Blick auf das Armaturenbrett eines beliebigen Autos: Die Geschwindigkeit wird – aus praktischen Gründen – analog angezeigt (Zeiger oder Balken vor einer Skala), die Anzeige des Kilometerstandes erfolgt digital (Zählwerk).
Es ist zu ergänzen, dass die elektronischen Bauteile des Computers binär (zweiwertig) arbeiten. 2 Diese Bauteile (genauer: ihre kleinsten Schalt- und Speicherelemente) können also jeweils einen von zwei Zuständen einnehmen, so wie ein elektrischer Schalter einen Stromkreis entweder unterbricht oder schließt. Das ist mehr als eine Metapher: Die Evolution des Computers führt von elektromechanischen Schaltern (Relais) über Röhren und Transistoren hin zu hochintegrierten Schaltkreisen, ohne dass sich die grundlegende Funktionsweise geändert hätte.
| physikalischer Zustand | digitale Bedeutung |
|---|---|
| kein Signal (0 V) | 0 |
| Signal (+5 V) | 1 |
In der Digitaltechnik kommen noch weitere Signalpegel zur Anwendung, aber das Ergebnis ist immer dasselbe: Null oder Eins.
Bereits mit dieser einen Ziffer, die man als ein Bit (von engl. binary digit: binäre Ziffer) bezeichnet, lässt sich eine Menge anfangen, wenn sie als logischer Wert interpretiert wird.
| digitale Bedeutung | logische Bedeutung |
|---|---|
| 0 | falsch |
| 1 | wahr |
Tatsächlich ist gerade die logische Bewertung von Aussagen (etc.) wesentliche Grundlage der Informationsverarbeitung. Das mathematische System dieser Aussagelogik wurde von dem englischen Mathematiker George Boole (1815 - 1864) entwickelt, weshalb es meist als Boolesche Algebra (technisch auch als Schaltalgebra) bezeichnet wird.
Auf eine ausführliche Darstellung dieses interessanten Systems sei hier verzichtet. Für den Überblick genügt die Feststellung, dass sich die Regeln und Funktionen dieser Algebra auf wenige Grundfunktionen reduzieren lassen, die in der Digitaltechnik elektronisch nachgebildet wurden (»Logikbausteine«).
In den Programmiersprachen sind diese Funktionen zumeist als logische bzw. bitweise Operatoren verfügbar:
NOT (Negation), AND (Konjunktion), OR (Disjunktion) und XOR (Antivalenz).
NOT kehrt einfach den binären Wert seines Operanden um. Es gilt also:
| NOT | Operand | Funktionswert |
|---|---|---|
| 0 | 1 | |
| 1 | 0 |
NOT hat – ein seltener Fall – nur einen Operanden. 3
Die anderen Operatoren haben zwei Operanden und liefern daher jeweils 4 mögliche Ergebnisse:
| AND | Operand 1 | Operand 2 | Funktionswert |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 1 | 0 | 0 | |
| 1 | 1 | 1 |
AND ergibt also dann 1, wenn beide Operanden den Wert 1 haben, sonst 0.
| OR | Operand 1 | Operand 2 | Funktionswert |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 1 |
OR ergibt bereits 1, wenn wenigstens einer der Operanden den Wert 1 hat.
| XOR | Operand 1 | Operand 2 | Funktionswert |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 |
XOR ergibt 1, wenn nur einer der Operanden den Wert 1 hat, sonst 0.
XOR (»eXclusive OR«) gehört eigentlich nicht mehr zu den Grundfunktionen und wird in der Programmierpraxis auch eher selten benötigt. 4
Während zur Darstellung eines Wahrheitswertes ein Bit ausreichend ist, erfordern Zahlenwerte natürlich fast immer mehrere solcher Binärziffern:
0 + 1 = 1
1 + 1 = 10
10 + 1 = 11
11 + 1 = 100
usw.
Lediglich solche Dualzahlen können durch die (binären) Schaltelemente verarbeitet werden. Der Computer verwendet mithin das Dualsystem. Dieses Zahlensystem, das auf den deutschen Philosophen und Mathematiker Gottfried Wilhelm Leibniz (1649 - 1716) zurückgeht, unterscheidet sich von unserem gewohnten Dezimalsystem im Grunde nur in der Zahlenbasis (2 statt 10).
Zahlensysteme und ‑darstellungen
Die Zusammenstellung zu einer Bitfolge potenziert die Anzahl möglicher Zustände, die diese Folge annehmen kann. Die Zusammenfassung von (in aller Regel) 8 Bits wird als Byte bezeichnet. Ein solches Byte kann 28 = 256 verschiedene Werte (von 0 bis 255) annehmen. Der Wertebereich einer Bitfolge verdoppelt sich mit jeder hinzugefügten Bitposition, durch 9 Bits lassen sich 512, durch 10 Bits 1024 Werte darstellen. 5
Dieser Sachverhalt ist uns allen von den Dezimalzahlen her vertraut: Mit einer Ziffer lassen sich 10 Werte (0 bis 9), mit zwei Ziffern 100 Werte (0 bis 99) darstellen. Hier verzehnfacht sich der Wertebereich mit jeder hinzukommenden Dezimalstelle.
Wenn b die Basis eines Zahlensystems und n die Anzahl der
Ziffern (Stellen) ist, ergibt dies allgemein bn Kombinationsmöglichkeiten mit einem Wertebereich von 0 bis bn − 1.
Beim Wechsel des Zahlensystems muss ein gegebener Zahlenwert selbstverständlich – von uns oder dem Computer – konvertiert, d.h. umgewandelt werden. 6 Die Umwandlung einer Bitfolge, also einer Dualzahl, in den dezimalen Wert ist recht umständlich, weil dabei der Dezimalwert jeder einzelnen Bitposition berechnet werden muss.
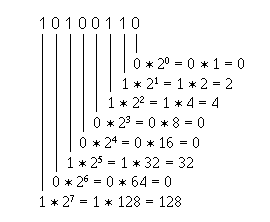
Der dezimale Wert ist also 2 + 4 + 32 + 128 = 166.
Dieselbe Schwierigkeit besteht natürlich umgekehrt bei der Umwandlung einer Dezimal- in eine Dualzahl. Andererseits ist für uns die Verwendung von Dualzahlen einfach zu unpraktisch. Die Dezimalzahl 1000 hat dual 10 Stellen und 10.000.000 (10 Mio.) bereits 20 Dualstellen. Wenn man aber ein Zahlensystem benutzt, dessen Basis eine Zweierpotenz ist und von 10 nicht weit entfernt liegt, dann werden die Konvertierungen deutlich vereinfacht und die Zahlengrößen bleiben überschaubar.
Diese Voraussetzungen werden von dem oktalen (Basis 8) und dem hexadezimalen (Basis 16) Zahlensystem erfüllt. 7 Das Oktalsystem ist dem Dezimalsystem näher, hat aber über die Jahre an praktischer Bedeutung verloren und spielt bei der PC-Programmierung fast keine Rolle. Deshalb wird hier nicht weiter darauf eingegangen.
Mit dem Gebrauch mehrerer Zahlensysteme kann es zu Unklarheiten kommen, daher müssen Zahlen ggfs. entsprechend gekennzeichnet werden. Die allgemeine Form besteht in der Anfügung eines Kleinbuchstabens:
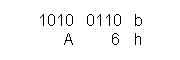
1000d = dezimal 1000
1000b = binär (dual) 1000 = 8d
1000o = oktal 1000 = 512d
1000h = hexadezimal ("hex") 1000 = 4096d
In Programmiersprachen existieren auch andere Kennzeichnungsformen, die typische BASIC-Form ist: 1000 (dezimal), &b1000 (dual), &o1000 (oktal) und &h1000 (hex.).
Um für das Hexadezimalsystem auf 16 Ziffern zu kommen, werden zusätzlich die Buchstaben A bis F (meist in Großschreibung) verwendet. Es gilt also:
9 + 1 = A (dezimal 10)
A + 1 = B (dezimal 11)
B + 1 = C (dezimal 12)
C + 1 = D (dezimal 13)
D + 1 = E (dezimal 14)
E + 1 = F (dezimal 15)
F + 1 = 10 (dezimal 16)
Die Umwandlung vom oder in das Dualsystem ist vergleichsweise einfach, weil je 4 Dualziffern (Bits) einer Hex-Ziffer entsprechen. 8 Für die obige Bitfolge erhalten wir:
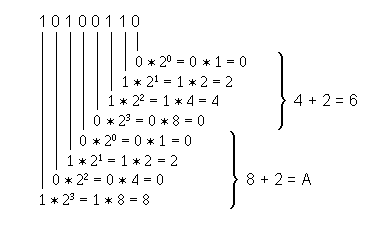
Der hexadezimale Wert ist A6.
Die Addition der Dualwerte erfolgt also nur noch für jede Hex-Ziffer.
Durch diese "Umrechnung in 4er-Gruppen" bereiten auch sehr große Dualzahlen kein Problem, während bei der Umwandlung in Dezimalzahlen immer mehr und zunehmend hohe Zwischenergebnisse auftreten. Noch deutlicher ist der Vorteil bei der Konvertierung in das Dualsystem. Der Dezimalwert 927 muss mühevoll »aufgeknackt« werden (fortlaufende Subtraktion der größten enthaltenen Zweierpotenz). Für 927h vereinfacht sich die Rechnung zu
9 = 1 * 23 (8) + 1 * 20 (1)
2 = 1 * 21 (2)
7 = 1 * 22 (4) + 1 * 21 (2) + 1 * 20 (1)
etc., aber in solch ausführlicher Form erscheint die Umwandlung komplizierter als sie ist. Stattdessen sollte man sich einfach das Schema der dualen Stellenwertigkeit 8–4–2–1 vor Augen halten, und es geht wie von selbst:
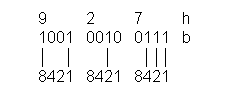
Anfangs sind diese »Zahlenspielereien« natürlich oft nervig und abschreckend. Als Programmierer hat man aber laufend mit dualen oder hexadezimalen Werten zu tun. Je besser man sich damit vertraut macht, umso leichter wird die praktische Arbeit.
Vergrößerungen
Um Zahlenwerte möglichst einfach (kurz) zu halten, gebrauchen wir ganz alltäglich bestimmte Vorsätze und Vorzeichen, die die Bedeutung eines Faktors haben, der gewissermaßen aus dem Zahlenwert »herausgenommen« wurde. So geben wir etwa eine größere Distanz in Kilometern (km), einen kleinen Längenwert bspw. in Millimetern (mm) an. Die bloße Verwendung der physikalischen Einheit Meter würde zu »unhandlichen« Zahlenwerten führen. Die Vorsätze Kilo und Milli entsprechen einem Faktor von 1000 (103) bzw. 1/1000 (10−3). Sehr große Werte lassen sich mit den Vorsätzen Mega (Faktor 106), Giga (Faktor 109) und Tera (Faktor 1012) etc. ausdrücken.
In Verbindung mit den Einheiten Bit und (vor allem) Byte sind die Vorsätze Kilo, Mega, Giga usw. auch in der EDV gebräuchlich. Allerdings haben sie hier in der Regel eine etwas andere mathematische Bedeutung:
| Vorsatz | Vorzeichen | Faktor |
|---|---|---|
| Kilo | K | 210 (= 1024) |
| Mega | M | 220 (= 1.048.576 = 1024 * 1024) |
| Giga | G | 230 (= 1.073.741.824 = 10243) |
Dies hat seinen Grund natürlich darin, dass die Faktorenwerte im Dualsystem abgebildet werden und die Zweierpotenzen ganzzahlige Exponenten haben sollen.
Das »EDV-Kilo« ist noch durch das großgeschriebene Vorzeichen erkennbar. Die anderen Vorsätze sind jedoch leider prinzipiell mehrdeutig, da sie in derselben Schreibweise auch im Dezimalsystem verwendet werden. 9 Um diese Unsicherheit auszuschließen, wurden für die EDV zusätzliche Binärpräfixe mit auf »bi« endenden Bezeichnungen definiert. Die (derzeit) wichtigsten sind:
| Vorsatz | Vorzeichen | Faktor |
|---|---|---|
| Kibi | Ki | 210 |
| Mebi | Mi | 220 |
| Gibi | Gi | 230 |
| Tebi | Ti | 240 |
Ganze Zahlen
Durch ein Byte (8 Bits) lassen sich 256 verschiedene Werte darstellen. Bezogen auf natürliche Zahlen hat ein Byte also einen Wertebereich von 0 bis 255. Anders gesagt, könnte die Zahl 255 (FFh) noch eben durch ein Byte repräsentiert werden. Das ist nicht sehr viel. Deshalb wird ein Byte ausgesprochen selten zur Repräsentation von Zahlenwerten verwendet.
Mit der Zusammenfassung von zwei Bytes (16 Bits) ergeben sich 65536 Werte, die größte darstellbare Zahl ist 65535 (FFFFh). Das ist für viele Belange ausreichend. Dieses Format ist für die Darstellung einer ganzen Zahl (engl. integer) weitverbreitet. 10 Für größere Zahlenwerte wird oft ein 32-Bit-Format verwendet, dessen Maximum dann schon bei 4.294.967.295 liegt. Zur eindeutigen Unterscheidung nennt man den 16-Bit-Typ short integer, der 32-Bit-Typ wird auch als long integer bezeichnet. 11
Beide Formate dienen wie gezeigt zur computergerechten Erfassung ganzer, positiver Zahlen. Wie aber lassen sich negative Werte darstellen?
Da das Vorzeichen selbst binären Charakter hat (plus oder minus), genügt ein Bit zu seiner Definition. Dieses Bit kann jedoch nicht einfach hinzugefügt werden, weil die Bitanzahlen grundsätzlich durch systemtechnische Größen – wie Speicherformate, s.u. – vorgegeben sind. Zur Darstellung einer vorzeichenbehafteten ganzen Zahl (signed integer) wird daher das höchstwertige Bit (MSB) herangezogen, wobei ein »gesetztes« Bit (Bitwert = 1) einem negativen Vorzeichen entspricht. Damit steht für den Zahlenwert (den absoluten Betrag) ein Bit weniger zur Verfügung, was den Wertebereich in etwa halbiert. Die größte positive Zahl im 16-Bit-Format ist nun 32767 (7FFFh), sonst ändert sich für positive Zahlen gar nichts.
Man könnte jetzt annehmen, dass sich auch für negative Zahlen nicht ändert, außer dass einfach noch das MSB gesetzt wird. Es wäre dann:
| 1 = 0001h | −1 = 8001h |
| 2 = 0002h | −2 = 8002h |
| usw. bis zu | |
| 32767 = 7FFFh | −32767 = FFFFh |
Leider ist diese Darstellungsform unbrauchbar! Das Problem besteht weniger im Vorhandensein einer »negativen Null« (8000h), als darin, dass einfache Additionen kein korrektes Ergebnis liefern:
| 00000000 00000111b = +7 10000000 00000101b = −5 |
| 10000000 00001100b = −12 |
Solche Fehler ließen sich nur vermeiden, wenn die Operation in anderer, aufwändigerer Weise durchgeführt würde. Es ist besser, zu Gunsten einfacher, effektiver Rechenoperationen ein anderes Zahlenformat zu wählen.
Hierzu wird die Darstellung einer negativen Zahl aus der positiven Zahl abgeleitet, indem alle Bits umgekehrt werden:
00000000 00000101b = +5
11111111 11111010b = −5
Wir kennen diese Umkehrung bereits als Negation (NOT-Operation, Inversion). Die umgekehrte (invertierte) Bitfolge wird auch als Komplement (Ergänzung) der ursprünglichen Folge bezeichnet.
Mit der somit erzielten Darstellungsform (sog. Einer-Komplement) ist das Problem unkorrekter Additionsergebnisse aber noch nicht zuverlässig beseitigt. Anders sieht es aus, wenn zu dem Komplement noch der Wert 1 addiert wird. Dies führt – endlich – zu der gebräuchlichen Darstellung negativer Ganzzahlen im sog. Zweier-Komplement:
00000000 00000101b = +5
11111111 11111010b = −5 im Einer-Komplement
11111111 11111011b = −5 im Zweier-Komplement
Durch diesen zusätzlichen Schritt wird übrigens auch das Vorkommen von −0 ausgeschlossen.
Wenn wir die nun gültige Übersicht der vorzeichenbehafteten 16-Bit-Ganzzahlen
| 1 = 0001h | −1 = FFFFh |
| 2 = 0002h | −2 = FFFEh |
| 3 = 0003h | −3 = FFFDh |
| usw. bis zu | |
| 32767 = 7FFFh | −32767 = 8001h |
| und: | −32768 = 8000h |
mit der Tabelle weiter oben vergleichen, mag uns die Darstellung negativer Zahlen irgendwie »unlogisch« oder zumindest »unelegant« erscheinen. Wir müssen uns damit abfinden, dass die erwähnten technischen Gründe zu dieser Darstellungsform geführt haben. 12
Bei anderen Integer-Formaten ergeben sich keine grundsätzlichen Abweichungen. Eine vorzeichenbehaftete 32-Bit-Integer hat demnach einen Wertebereich von −2147483648 (80000000h) bis 2147483647 (7FFFFFFFh).
»Überläufer«
Nun stellt sich natürlich die Frage, wie mit Zahlenwerten verfahren wird, die nicht (mehr) zum eingesetzten Integer-Format passen. Nehmen wir zum Beispiel an, wir verwenden den eben behandelten Datentyp 16-Bit-Integer. Wie wird dann das Ergebnis von 32767 + 1 gespeichert?
Grundsätzlich lässt sich die Addition durchführen: Der Wert 7FFFh erhöht sich zu 8000h. Bei einer vorzeichenlosen Integer (unsigned integer) ist dieses Ergebnis auch korrekt darstellbar (dezimal: 32768). Hingegen ist beim vorzeichenbehafteten Typ das Ergebnis falsch (−32768). Ein ähnliches Problem ergibt sich, wenn das Rechenergebnis überhaupt nicht mehr darstellbar ist: FFFFh + 1 = 10000h. Bezogen auf das Datenformat führen diese Berechnungen also zu einem Überlauf (engl. overflow).
Was bei einem Überlauf nun tatsächlich passiert, hängt vom Programm ab, das die Rechenoperation durchführt. Der Regelfall ist sicher, dass der Überlauf erkannt und in irgendeiner Weise als Fehler behandelt wird. Es ist aber auch denkbar, dass ein Programm diesen Überlauf ignoriert und einfach den – ggfs. abgeschnittenen – Ergebniswert speichert. Im zweiten Fall würde aus 10000h also 0000h (= 0).
Dieses Abschneiden wird übrigens nicht vom Programm vorgenommen (jedenfalls normalerweise nicht), sondern erfolgt automatisch mit der Rechenoperation bzw. der Ergebnisspeicherung. 13 Für den Zahlenwert muss ja eine Speicherstelle reserviert werden, deren Größe vom verwendeten Datentyp bestimmt ist, im Beispiel also 16 Bits (2 Bytes). Diese Speicherstelle kann nicht einfach so nach Bedarf wachsen. Und sie kann auch nicht beliebige Größen annehmen, weil – wie oben bereits erwähnt – aus technischen Gründen nur bestimmte Datenformate möglich sind. Dies wird später noch genauer betrachtet.
Gleitkommazahlen
Neben den Ganzzahlen gibt es eine zweite wichtige Gruppe numerischer Datentypen, die als Gleitkommazahlen oder Gleitpunktzahlen (engl. floating point numbers), mitunter auch als Fließkommazahlen bezeichnet werden. Hier kommt zum Ausdruck, dass als Trennzeichen in Dezimalbrüchen – international gesehen – der Punkt oder das Komma verwendet wird. Der Begriff Gleitkommazahl folgt also der deutschen Notation. In Programmiersprachen ist allerdings entsprechend der angloamerikanischen Schreibweise der Dezimalpunkt gebräuchlich!
Mathematisch handelt es sich dabei um rationale Zahlen. Ihre Codierung als Datentypen ist genormt (IEEE) und umfasst 32, 64 oder 80 Bits. 14
Die Terminologie für diese Typen ist allerdings unterschiedlich, die BASIC-Bezeichnungen single, double und ext (extended) beziehen sich auf die Präzision der Zahlendarstellung, während andere Bezeichnungen oft auf die Bitbreite abstellen:
| 32 Bit | single (precision) | short real |
| 64 Bit | double (precision) | long real |
| 80 Bit | extended (precision) | temp real |
Real numbers (reelle Zahlen) ist gleichfalls eine verbreitete (mathematisch nicht ganz exakte) Bezeichnung für diese Datentypen.
Gleitkommazahlen werden grundsätzlich für alle nicht ganzzahligen Werte herangezogen, also Werte wie bspw. 365,25 oder 1,95583. Bei der Betrachtung dieser »Kommazahlen« drängt sich natürlich die Frage auf, wie solche – eben recht unterschiedliche – Zahlenwerte in demselben, festen Format erfasst werden sollen. Es gibt aber eine gebräuchliche, einfache Methode für diese »Formatierung«: die Normalisierung. Hierbei wird die Zahl als Produkt eines Dezimalbruchs (Mantisse) und einer dezimalen Potenz dargestellt. Die allgemeine Form ist
Mantisse * 10Exponent
wobei der Betrag der Mantisse größer oder gleich 0,1 und kleiner 1 ist. Der Exponent ist eine ganze Zahl. Ist die Basis festgelegt, so bleiben nur Mantisse und Exponent als relevante Größen. Bei einer vereinfachten Schreibweise werden daher Multiplikation und Basis (10) durch den Buchstaben E ersetzt, nicht selten wird auch noch die führende Null der Mantisse weggelassen.
| gewöhnliche Darstellung | normalisierte Form | Exponentialformat |
|---|---|---|
| 365,25 | 0,36525 * 103 | 0,36525E3 |
| 1,95583 | 0,19558 * 101 | 0,19558E1 |
| 0,00029088821 | 0,29088821 * 10−3 | 0,29088821E−3 |
Computerintern werden Gleitkommazahlen also in normalisierter Form dargestellt. Allerdings handelt es sich dort selbstverständlich um eine binäre Repräsentation des Zahlenwertes, Mantisse und Exponent sind daher Dualzahlen!
Mit diesem Unterschied – und weiteren Details des IEEE-Formats – wollen wir uns hier aber nicht mehr befassen,
zumal solche Kenntnisse so gut wie nie benötigt werden. Für die Praxis ist etwas anderes viel bedeutsamer!
Während ganze Zahlen im Rahmen des formatspezifischen Wertebereichs stets exakt darstellbar sind, ist dies bei Gleitkommazahlen leider aus zwei Gründen nicht der Fall. Zuerst einmal führt jedes feste Längenformat bei Gleitkommazahlen zu einer Beschränkung nicht nur der Zahlengröße sondern auch der Genauigkeit (Präzision). Im 32-Bit-Format lassen sich etwa 6 bis 7 Dezimalstellen genau darstellen, eine größere Stellenanzahl führt zu einer Ungenauigkeit durch Rundung. Neben einem Überlauf (Overflow) kann es bei der Speicherung von Gleitkommazahlen somit auch zu einem »Unterlauf« (Underflow) kommen: Ein sehr kleiner, nicht mehr darstellbarer Zahlenwert wird zu Null gerundet.
Die zweite Ursache für Ungenauigkeiten liegt in der Konvertierung der Zahl vom Dezimal- in das Dualsystem. Manche Dezimalzahlen können nämlich nicht exakt als duale Gleitkommazahlen dargestellt werden.
Durch Verwendung »breiterer« Formate lassen sich solche Ungenauigkeiten zwar vermindern aber nicht prinzipiell ausschließen. Für die meisten Anwendungen sind diese Datentypen allerdings hinreichend genau. Lediglich in bestimmten Fällen, etwa bei extremen Werten oder einer Akkumulation der Fehler durch (wiederholte) Rechenoperationen kann es zu unbrauchbaren Ergebnissen kommen. Darauf muss man als Programmierer achten und ggfs. auf andere Datentypen ausweichen. 15
Zeichen und Texte
Bisher haben wir nur numerische Daten betrachtet. Dies ist tatsächlich die einzige Datenform, die ein Computer verarbeiten kann. Wir wissen aber (und erwarten), dass ein Computer auch zur Ein- und Ausgabe von Texten befähigt ist. Es ist klar, dass jedes Textzeichen hierzu durch einen numerischen Wert repräsentiert werden muss. Für den PC existieren im Wesentlichen drei Normen der numerischen Codierung von Zeichen: ASCII, ANSI und Unicode.
ASCII (American Standard Code for Information Interchange) ist hiervon die älteste Norm, wobei es sich eigentlich um einen 7-Bit-Code (128 Werte) handelt. IBM hatte diesen bei der Einführung des PC auf 8 Bit (also 1 Byte, 256 Werte) erweitert und die hinzugewonnene obere Hälfte nach eigenem Gutdünken zur Codierung nationaler Sonderzeichen u.a. genutzt. Mit der Bezeichnung OEM-Zeichensatz (OEM: Original Equipment Manufacturer) wird zum Ausdruck gebracht, dass diese Codierung nicht genormt, sondern vom Systemhersteller abhängig ist. Daneben existieren noch andere ASCII-Erweiterungen, insb. mehrere ISO-Normen (ISO: International Organization for Standardization).
Der ANSI-Zeichencode (ANSI: American National Standard Institute) ist eine (ISO-konforme) ASCII-Erweiterung. Durch die Verwendung in Windows hat der ANSI-Zeichencode besondere Bedeutung erlangt.
Beiden (bzw. allen) 8-Bit-Codes ist gemeinsam, dass ihre Kapazität von 256 Zeichen eigentlich zu beschränkt ist, zumal die ASCII-Werte 0 bis 31 Steuercodes darstellen. Schon mit der Berücksichtigung aller lateinischer Schriftzeichen der europäischen Sprachen und einiger Symbole von internationaler Bedeutung wird die Grenze erreicht.
Eine Möglichkeit, diese Beschränkung zu umgehen, ist der Wechsel zwischen verschiedenen Zeichensätzen, wobei die eindeutige Zuordnung eines Codewerts zu einem bestimmten Zeichen aufgehoben wird. Die im PC-Betriebssystem DOS implementierten Codepages definieren Zeichensätze, die sich in der oberen Codehälfte unterscheiden. Im Grunde ist dies aber nur als Notbehelf zur Anpassung an (einige) nationale Gegebenheiten zu sehen.
Graphisch orientierte Betriebssysteme können natürlich noch einen großen Schritt weiter gehen, indem die Darstellung eines Zeichens von einem Muster oder einer Beschreibung (Font) bestimmt wird. Damit ist der Wechsel
zwischen Zeichensätzen auch innerhalb derselben Anwendung möglich.
Solche Lösungen sind aber prinzipiell nur für einzelne Systeme zureichend, da sie die Grenzen eines 8-Bit-Codes nicht
wirklich aufheben können. Die Mehrdeutigkeit eines Codewerts stellt immer einen Informationsverlust dar, der den Austausch von Informationen zwischen Systemen be- oder gar verhindert.
In Zeiten des globalen Informationsaustausches (und der globalen Vermarktung) sind letztlich alle Schriften, auch die gänzlich anderer Sprachkulturen zu berücksichtigen. Wenn man bedenkt, dass die chinesische Schrift über 40000 Zeichen kennt, wird einem die Größenordnung dieses Unterfangens deutlich.
Diesem Ziel widmete sich ab 1983 eine ISO/IEC-Kommission (IEC: International Electrotechnical Commission) mit der Entwicklung eines 4-Byte-Codes. Noch während dieser Arbeit entstand aus privater Initiative ein 2-Byte-Code namens Unicode, an dessen Definition schließlich alle großen Computerfirmen und eine Gruppe wissenschaftlicher Bibliotheken mitwirkten. Aufgrund einer engen Zusammenarbeit zwischen dem Unicode-Konsortium und der ISO/IEC-Kommission wurde Unicode ein Bestandteil (UCS) der 1992 erschienenen Zeichensatznorm ISO 10646. Beide Standards sind inzwischen praktisch identisch und befinden sich weiter in der Entwicklung. Jedenfalls hat sich Unicode/UCS als Universalzeichensatz durchgesetzt und wird von allen zeitgemäßen Betriebssystemen verwendet bzw. unterstützt.
Für die systemtechnische Verwendung des Zeichensatzes existieren bestimmte Zeichencodierungen (Unicode Transformation Format, UTF), die sich in Codierungsdetails unterscheiden. Die für PC-Systeme wichtigsten Formate sind:
| UTF-8 | 1 bis 4 Bytes | sehr verbreitet (Unix u.a.), ASCII-kompatibel, bedeutsam für Internet-Protokolle |
| UTF-16 | 2 (oder 4) Bytes | gleichfalls sehr verbreitet (Windows, OS X, u.a. Umgebungen) |
| UTF-32 | 4 Bytes | besonders einfache Codierung, jedoch relativ selten eingesetzt |
Bei der computerinternen Verarbeitung und Speicherung von Unicode-Zeichen in Form von 16- oder 32-Bit-Integer stellt sich – wie später noch beim Thema Speicherformate erklärt wird – das Problem, dass die Bytereihenfolge bei UTF-16 und UTF-32 nicht eindeutig festliegt. (Bei UTF-8 wird dies durch die Art der Codierung vermieden.) Daher kann die Bytereihenfolge für einen Unicode-Text durch eine vorangestellte Markierung (byte order mark, BOM) signalisiert werden. Dabei handelt es sich um ein spezielles Unicode-Zeichen. Die UTF-Bezeichnungen werden ggfs. um das Kürzel »BE« (Big-Endian) oder »LE« (Little-Endian) ergänzt. Auch diese Begriffe werden weiter unten erläutert.
Bitmasken und Maschinenformate
Bei den vorgestellten Datentypen können wir (vereinfachend) die Bitfolge als eine Einheit betrachten, selbst wenn dabei einzelnen Bits eine besondere Bedeutung zukommt, wie etwa dem höchstwertigen Bit (MSB) einer vorzeichenbehafteten Integer. Es ist aber auch möglich, einen Datentypen so zu definieren, dass Teile der Bitfolge – oder sogar jedes einzelne Bit – eine besondere Bedeutung haben. (Dies ist bei dem Statusregister des Prozessors der Fall.) Solche verwendungspezifischen Bitfolgen werden oft Binärmuster oder Bitmasken genannt. Sie ermöglichen die Platz sparende Zusammenfassung von Informationen, die binär (einzelne Bits) oder durch sehr kleine Zahlenwerte (mehrere Bits) darstellbar sind.
Wer sich etwa mit dem Windows-API beschäftigt, findet dort Bitmasken in Hülle und Fülle. Hier ein Beispiel aus einer älteren Deklarationsdatei für Visual Basic:
' OpenFile() Flags Public Const OF_READ = &H0 Public Const OF_WRITE = &H1 Public Const OF_READWRITE = &H2 Public Const OF_SHARE_EXCLUSIVE = &H10 Public Const OF_SHARE_DENY_WRITE = &H20 Public Const OF_SHARE_DENY_READ = &H30 Public Const OF_SHARE_DENY_NONE = &H40 Public Const OF_PARSE = &H100 Public Const OF_DELETE = &H200 Public Const OF_VERIFY = &H400 Public Const OF_CANCEL = &H800 Public Const OF_CREATE = &H1000 Public Const OF_PROMPT = &H2000 Public Const OF_EXIST = &H4000 Public Const OF_REOPEN = &H8000
Wenn wir alle oben aufgeführten Werte verknüpfen, so ergibt sich diese Bitfolge:
1111 1111 1111 0011
Man sieht sofort, dass zwei von 16 Bitpositionen hier nicht verwendet werden. Alle übrigen Bits sind im Beispiel gesetzt, d.h. sie haben den Wert 1. Welche Kombination jedoch tatsächlich möglich bzw. sinnvoll ist, hängt natürlich von der Definition im realen Einzelfall ab.
Die Binärinformation (und auch der sie enthaltende Datentyp) wird gerne als Flag (engl.; Flagge, Fahne) bezeichnet, was anschaulich auf den Signalcharakter hinweist. Die Auswertung von Flags erfolgt durch logische bzw. Bit-Operationen (insb. AND), seltener durch numerische Vergleiche. So könnte die Integer openflags mit einer Anweisung wie
openflags = OF_READ or OF_EXIST
zwei der definierten Binärinformationen enthalten. Und eine logische Auswertung der Operation
openflags and OF_EXIST
würde zeigen, ob das Flag OF_EXIST gesetzt ist. Hingegen dürfte der Ganzzahlwert von openflags in der Regel ziemlich uninteressant sein.
Es liegt auf der Hand, dass auch solche Bitstrukturen – ebenso wie Datenobjekte überhaupt – nicht beliebige Größen haben können, sondern an Speicherformate (und Prozessor-Eigenschaften) eines Computers gebunden sind.
Die kleinste Einheit, die im Speicher angesprochen (»adressiert«) werden kann, ist ein Byte. Selbst ein einzelnes Bit lässt sich daher nur als Byte speichern, weil die Speicherstelle Bytegröße hat. Das Format eines größeren Datenobjekts besteht folglich aus dem Vielfachen eines Bytes. Die nächstgrößere Einheit, die zusammenhängend verarbeitet werden kann, wird als Word (Wort, oft in der Schreibweise »WORD«) bezeichnet. Sie setzt sich aus 2 Bytes (16 Bits) zusammen. 16 Byte und Word stellen sozusagen elementare Maschinendatentypen dar. Mit dem Double-Word (Doppelwort, DWORD) und anderen Typen werden noch größere Einheiten definiert.
Einfache (skalare) Datentypen entsprechen unmittelbar bestimmten »Maschinenformaten«:
| short integer (16-Bit) | WORD |
| long integer (32-Bit) | DWORD |
| single precision float | DWORD |
Man sieht aber, dass es falsch wäre, von einer Identität zu sprechen. Das DWORD-Format impliziert offensichtlich keinen eindeutigen Datentyp. Und ob ein WORD nun eine Integer mit oder ohne Vorzeichen, ein Unicode-Zeichen oder etwa ein Binärmuster darstellt, lässt sich aus dem Format allein nicht schließen.
Diese maschinennahen Formate sind für Programmierer allerdings nicht immer als Datentypen verfügbar. Vor allem das Fehlen eines Typs WORD bzw. DWORD als vorzeichenloser Integer macht sich in der Praxis unangenehm bemerkbar, weil bestimmte positive Werte dann nur recht umständlich verarbeitet werden können. 17
Endianess
Im Prinzip kann man davon ausgehen, dass Daten byteweise abgelegt werden. Jedoch ist die Speicherung von Integertypen – es wurde weiter oben schon angedeutet – noch mit einer Besonderheit »geschlagen«. 18 Gehen wir von einer 16-Bit-Integer aus, die den Zahlenwert 4660 hat. In hexadezimaler Darstellung, die dem tatsächlichen Speicherformat besser entspricht, ist das der Wert 1234h. Wir würden also die folgende Speicherung erwarten:
| Speicherstelle | Speicherinhalt |
|---|---|
| 1 | 12 |
| 2 | 34 |
Bei dieser Abfolge liegt der höherwertige Datenteil (nämlich der Wertebereich 28 bis 215) an der kleineren Speicheradresse, der geringerwertige Datenteil (20 bis 27) an der höheren Speicheradresse. Diese als Big-Endian bezeichnete Abfolge ist durchaus verbreitet, wird jedoch nicht in der Prozessortechnik des Herstellers Intel eingesetzt. Daher findet sich auf PC-Systemen die umgekehrte Bytefolge
| Speicherstelle | Speicherinhalt |
|---|---|
| 1 | 34 |
| 2 | 12 |
wobei an der höheren Speicheradresse der signifikantere Datenteil abgelegt ist (Little-Endian). 19
Von dieser unterschiedlichen Speicherabfolge – man spricht in dem Zusammenhang auch von Endianess – sind in aller Regel die größeren Datentypen entsprechend betroffen:
| Endianess | Speicherinhalt | |||
|---|---|---|---|---|
| Big-Endian | 12 | 34 | 56 | 78 |
| Little-Endian | 78 | 56 | 34 | 12 |
Üblicherweise spielt die Bytefolge in der Programmierung nur dann eine Rolle, wenn eben explizit auf den Bestandteil eines Datentypen zugegriffen werden soll.
Komplexe Datentypen, Datensätze
Einfache Datentypen können kombiniert werden, wodurch zusammengesetzte Datentypen entstehen. Die Möglichkeiten und Details hängen hierbei nicht wenig von der konkreten Systemumgebung und insb. Programmiersprache ab. Sehr häufig wird ein komplexer Datentyp durch die Aneinanderreihung desselben einfachen Typs gebildet. Das ist beispielsweise bei Texten der Fall, deren zugrunde liegender Datentyp eine Zeichenkette (String) ist. Der Begriff veranschaulicht bereits, dass hierbei einzelne Zeichen, d.h. Codewerte, verknüft werden. Ein in ANSI codierter Text ist also durch eine Kette von Bytes repräsentiert.
Diese einfache Form der Textspeicherung als Feld (Array) von Zeichencodes findet sich etwa in der Programmiersprache C. In BASIC wurde hingegen schon früh ein erweiterter Datentyp String verwendet, bei dem – vereinfacht gesagt – den Textdaten noch eine Längeninformation vorangestellt wurde. Damit haben wir es hier schon mit einer Zusammenstellung unterschiedlicher Datentypen zu tun.
Die Verbindung verschiedener Datentypen ist weit verbreitet, da es hierfür sehr viele Anwendungen gibt. Allgemein bezeichnet man diesen Verbund als Datensatz, auch Struktur (structure, struct) und Record sind geläufige Bezeichnungen. Ein recht typischer Fall der praktischen Verwendung ist die Zusammenstellung von Adressdaten, wie Name, Anschrift und weitere Informationen in einem Datenobjekt. Hiervon zu unterscheiden ist aber die logische Verknüpfung getrennter Datenobjekte, wie sie etwa in vielen Datenbanken erfolgt.
Anmerkungen:
1) »Computer« bedeutet schließlich nicht anderes als Rechner (engl. to compute: [be]rechnen). Dies sei auch deshalb erwähnt, weil manchmal darin eine Art »Denkmaschine« oder elektronisches Orakel gesehen wird.
2) Die Begriffe binär und dual werden, gerade in diesem Zusammenhang, häufig synonym gebraucht, was nicht ganz korrekt ist. (Binär hat als Fachwort noch weitere Bedeutungen.)
3) Ein solcher Operator wird als unär oder unitär bezeichnet. Da NOT die Bitwerte umgekehrt, nennt man diese Operation mitunter auch Inversion (Umkehrung).
4) XOR wird hauptsächlich dazu benutzt, um Bitmuster gezielt zu verändern und, einfach durch nochmalige Anwendung, wiederherzustellen. Die wichtigsten Einsatzbereiche sind bestimmte Graphikfunktionen und die Datenverschlüsselung.
5) Für die Zusammenstellung von 8 Bits existiert auch die Bezeichnung Oktett.
Die Ausdrücke most significant bit (MSB) und least significant bit (LSB) beziehen sich auf das Bit der höchsten bzw. niedrigsten Wertigkeit einer Bitfolge. (Mitunter werden dieselben Abkürzungen auch für die entsprechenden Bytes in einem Multi-Byte-Objekt, z.B. einem Word, verwendet.)
6) In der EDV bezeichnet Konvertierung allgemein eine Umwandlung von Daten (seltener von Programmcode), insb. die Überführung in ein anderes Format.
7) Die sprachlich korrekte Bezeichnung sedezimal (statt hexadezimal) wird ziemlich selten verwendet. Hingegen ist die Kurzform »Hex« (z.B. »Hex-Zahl«) recht gebräuchlich.
8) Eine solche Folge von 4 Bits wird als Tetrade, ferner auch als Half-Byte oder Nibble bezeichnet.
9) Die Hersteller von Festplatten haben sich dies schon früh zunutze gemacht, indem sie bei Kapazitätsangaben die dezimalen Faktoren – und nicht die für Speichergrößen eigentlich üblicheren Dualwerte – zugrunde legen, was zu höheren Zahlenwerten führt.
10) Das Wort Integer wird gerne (auch von mir) wie ein deutsches Substantiv gebraucht, gleichfalls die Kurzform »Int«.
Ich bin bestimmt kein Freund anglisierender Neologismen, aber einige Begriffe lassen sich nur schwer übersetzen oder verlieren dabei ihre klare Bedeutung. Wer ein wenig Programmierpraxis hinter sich hat, weiß, was eine »Longint« ist. Dann kommt man bei »langer Ganzzahl« schon eher ins Grübeln.
11) Die Notwendigkeit einer solchen Unterscheidung hat nicht nur sprachliche Gründe. Auf vielen Systemen existieren mehrere Integer-Formate, auf PC-Systemen etwa die genannten Formate 16- bzw. 32-Bit sowie in der Regel auch noch ein neueres 64-Bit-Format. Die genaue Bedeutung der Datentypbezeichnungen hängt durchaus von der jeweiligen Systemumgebung ab! Der Begriff long integer kann sich daher auch auf den 64-Bit-Typ beziehen, der andererseits oft als long long bezeichnet wird.
12) Ergänzend ist festzuhalten, dass die Vorherrschaft des Zweier-Komplements für Mikrocomputer wie den PC gilt, aber nicht für alle Computersysteme vorausgesetzt werden darf.
13) Es ist allerdings auch möglich, dass eine solche Speicherung vollständig erfolgt und dabei eine benachbarte Speicherstelle mitbenutzt, die eigentlich für einen anderen Verwendungszweck vorgesehen ist. Im Prinzip eine geradezu klassische Fehlerursache!
14) Der Typ erweiterte Gleitkommazahl (80 Bits) ist in Programmiersprachen nicht immer implementiert.
Der IEEE-Norm (IEEE: Institute of Electrical and Electronics Engineers) zur Darstellung von Gleitkommazahlen wird auf vielen Systemumgebungen entsprochen, so dass dieses Format das wichtigste ist. Für den PC existieren allenfalls historisch bedingte Abweichungen:
In früheren BASIC-Versionen von Microsoft wurde ein eigenes (proprietäres) Speicherformat (Microsoft Binary Format, MBF) verwendet. In Turbo Pascal (Borland) wurde ein zusätzlicher, proprietärer Datentyp »Real« implementiert.
15) Eine Lösung stellen die binär codierten Dezimalzahlen (BCD) dar. Weil dieser Datentyp jedoch häufig nicht verfügbar ist, gehe ich hier nicht weiter darauf ein.
16) Da Speicher- und Operandenformate maschinenabhängig sind, treffen die angegebenen »Breiten« (Bit- bzw. Byteanzahlen) keineswegs auf alle Computersysteme zu. Die hier genannten Werte gelten für den PC und weitere Mikrocomputer.
17) Gerade frühere BASIC-Dialekte litten an dem Problem, dass deren Integertypen grundsätzlich vorzeichenbehaftet waren.
18) Grundsätzlich kann Endianess auch andere Datentypen betreffen, soweit deren Datenteile einzeln adressierbar sind, also insb. an diskreten Speicherstellen des Computersystems abgelegt werden. Neben den beiden hier dargestellten Varianten existieren auch seltenere Mischformen. Bei einer Reihe von Systemen (Prozessoren) lässt sich die Bytefolge umschalten (sog. Bi-Endian).
19) Die Begriffe Big-Endian/Little-Endian entstammen dem satirischen Roman Gullivers Reisen des irischen Schriftstellers Jonathan Swift (1667 - 1745). Dort wird ein gesellschaftlicher Konflikt beschrieben, der auf der Frage basiert, ob ein gekochtes Ei richtigerweise am spitzen oder am breiten Ende geöffnet (aufgeschlagen) werden soll.


